Experimental ProxImaL intermediate representation¶
Note
This feature is currently work in progress.
The proximal.experimental namespace introduces a new internal representation
(IR) for describing optimization problems in ProxImaL. Loosely mirroring the
LLVM and Halide projects, the IR provides a unified foundation for problem
rewriting, problem formulation rendering, and code generation. It replaces a
number of common code paths previously scattered across proximal.* with a
single, consistent architecture.
The IR is implemented using Python dataclass structures (Python 3.11+). All
problem-level transformations, including grouping, absorption, splitting, and
diagonal scaling, operate exclusively on these IR objects should the end user
chooses to adopt the new ProxImaL syntaxes.
Image distortion models and the corresponding image reconstruction problem
formulation can be directly composed with the IR objects, albeit with a very
verbose code. To aid the transition, a minimal parser is available at
px.experimental.frontend.parser. This “easy mode” allows users to write
simple optimization problems using a lightweight external domain-specific
language (DSL) similar to the original language syntax at
proximal.prox_fns.*, and proximal.lin_ops.*.
Quick start¶
The following example (from examples/test_proximal_lite.py) shows
how to define a problem using the experimental frontend and apply the
built-in rewriting pipeline:
problem = parse(
"""
sum_squares(conv(k, u) - b) +
1.0e-5 * group_norm(grad(u)) +
1.0e-3 * sum_squares(grad(u)) +
nonneg(u)
""",
variable_dims=dims,
const_buffers={"b": np.ones(out_dims),
"k": np.ones((N, N), order="F", dtype=np.float32) / (N*N)},
)
print("Before:\n", problem)
optimized_problem = scale(split(group(absorb(problem))))
print("After:\n", optimized_problem)
Visualization of the ProxImal-IR¶
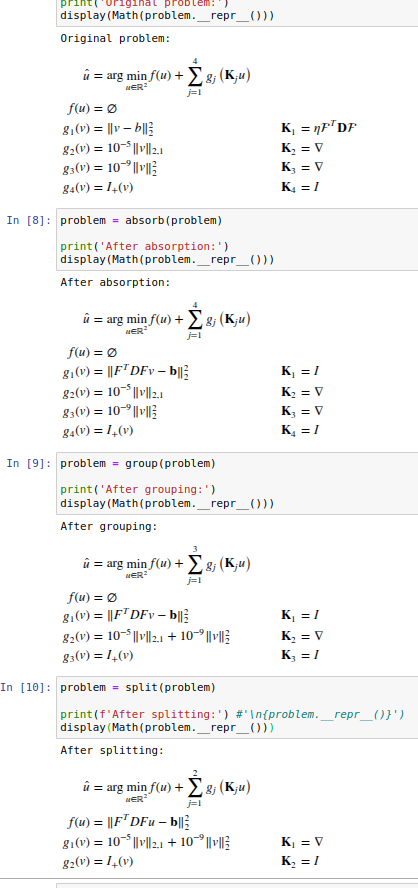
Screenshot of the LaTeX Math equations for each problem rewriting step.¶
Rationale¶
The experimental IR addresses several limitations in the previous design:
Problem rewriting behavior is now predictable and uniformly defined.
Grouping, absorption, and scaling logic are implemented in single, consolidated modules.
Visualization uses symbolic LaTeX rendering for clearer inspection of mathematical expression, step-by-step from absorption to splitting and scaling.
The IR directly supports future code-generation targets, including Halide and PyCUDA.
Warning
Advanced problem formulations, e.g. multi-channel image deconvolution and/or poisson deconvolution, are work in progress.
The new IR simplifies inspection of intermediate problem forms, which is especially useful when tuning deep signal distortion pipelines.
Comparison with the previous architecture¶
The following table summarizes major differences between the legacy system
(proximal.*) and the experimental IR:
Feature |
Previous System ( |
Experimental IR ( |
|---|---|---|
Stability |
✅ Stable |
Experimental; API may change |
Typical usage |
Academic benchmarking |
✅ Code generation and deployment on embedded hardware |
Visualization |
Graph-based operator DAG |
✅ LaTeX equation rendering |
Grouping logic |
Requires explicit, carefully structured user code |
✅ Automatic grouping via IR hashing |
Absorption rules |
Distributed across multiple algorithm modules |
✅ Centralized in |
Diagonal scaling |
Spread across several algorithm files |
✅ Centralized in |
Halide/PyCUDA support |
✅ Working implementations for PyCUDA, Numpy, Numexpr, and Halide. |
Unstable; Hybrid Halide & Numpy for simulation; pure Halide output for baremetal targets. |
Extendability |
✅ Easy to add new operators and prox functions |
Experimental; custom ops become black-box IR nodes |
Planned development roadmap¶
The following features are planned or in progress:
Component |
Status |
Notes |
|---|---|---|
Numpy solver backend |
To be implemented |
Will utilize IR for execution |
PyCUDA backend (operator graph) |
Planned |
IR representation may remove the need for explicit graph building |
PyCUDA kernel generation |
Planned |
Likely under |
Halide code generation |
Supported experimentally |
Uses IR as the canonical input |
Custom linear/prox operators |
Limited support |
IR will treat unknown operators as black-box nodes |
The experimental IR provides the foundation for future compilation targets, including pure Halide pipelines and optimized embedded-device execution.